2.3.3 Integral de x elevada a la n

2.3.3 Integral de x elevada a la n

Si la función a integrar es x, las fórmulas de integración son

Descubridor: Cavalieri (1598-1647)

Demostró: (n=1,2..9) Cavalieri; (n=entero positivo)

Demostración #1: Desde la derivada

Dando : 

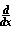1. x^{^m} = m x^{^(m-1)}
2. El teorema fundamental de cálculo

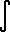
m x^{^(m-1)} dx =  x^{^m} dx = x^{^m} + d. (El Teorema fundamental

de cálculo (d = una constante arbitraria)

x^{^(m-1)} dx = x^{^m} / m + c (Divida ambos lados por m)

(c=una constante arbitraria, d/m = c)

x^{^n} dx = x^{^(n+1)} / (n+1) + c (Fije m=n+1, substitución) QED.

Demostración #2: El método de Fermat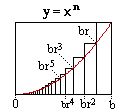

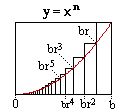
Siendo:

1. 1 + r + r^{^2} + .. + r^{^n} = (1 - r^{^(n+1)}) / (1-r)
2. 1 + r + r^{^2} + ... = 1 / (1-r) (r < 1)

(0 to b) x^{^n} dx es computado por tomando las áreas de un número infinito de

          subintervalos; subintervalos mas grandes a xcerca de b, mas pequeños cuando
          cerca de 0.

(0 to b) f(x) dx = f(b)*(b - br) + f(br)*(br - br^{^2}) + f(br^{^2})*(br^{^2} - br^{^3}) + ... (r -> 1-)

= b^{^n}*(b - br) + (br)^{^n}*(br - br^{^2}) + (br^{^2})^{^n}*(br^{^2} - br^{^3}) + ...

= b^{^(n+1)}(1-r) + b^{^(n+1)}r^{^(n+1)}(1-r) + b^{^(n+1)}r^{^(2n+2)}(1-r) + ...

= b^{^(n+1)}(1-r) [ 1 + r^{^(n+1)} + (r^{^(n+1)})^{^2} + ... ]

= b^{^(n+1)}(1-r) [ 1 / (1-r^{^(n+1)}) ] (Teorema 2.)

= b^{^(n+1)} / [ (1 - r^{^(n+1)}) / (1-r) ]

= b^{^(n+1)} / [ 1 + r + r^{^2} + .. + r^{^n} ] (Teorema 1.)

= b^{^(n+1)} / (n+1) (r -> 1) QED.

https://www.youtube.com/watch?feature=player_embedded&v=yXN6H5lg054