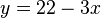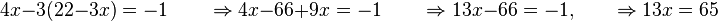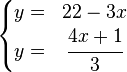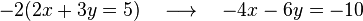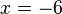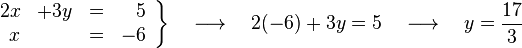Pues en este semestre de matemáticas para administración aprendimos mucho, para llevar acabo estas aplicaciones matemáticas en nuestra o la empresa donde se trabajara o se toman decisiones esto nos ayudara y servirá de mucho para determinar los costos, utilidades, consumo, ahorro, excedentes del consumidor y del productor, valor presente, valor futuro, insumo-producto, análisis de ventas, y comportamiento del consumidor, de antemano muchas gracias por visitar y ver mi blog`
jueves, 27 de noviembre de 2014
4.4 Aplicaciones :Modelo insumo-producto, análisis de ventas y comportamiento del consumidor.
4.4 Aplicaciones :Modelo insumo-producto, análisis de ventas y comportamiento del consumidor.
A fin de presentar en las siguientes líneas la esencia del modelo de Insumo–Producto, imaginemos una economía sin comercio exterior y sin impuestos, para simplificar la exposición. Pensemos en una matriz insumo–producto esquemática como la que se muestra a continuación (véase Leontief, 1986 y Millery Blair, 1985).
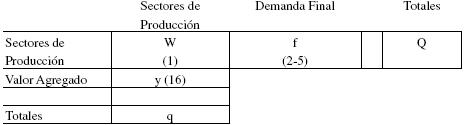
Donde el elemento típico de W es Wij, que representa las ventas del sector i al j, f es un vector columna que muestra las ventas del sector i a la demanda final y y es un vector hilera que muestra los pagos del sector j a los factores de producción.
Entonces, la matriz insumo producto se puede representar alternativamente como:

que no es más que una representación de la matriz insumo producto en términos de flujos.
Definamos ahora Wij = aij qj , es decir el coeficiente aij = Wij / qj , y tenemos:
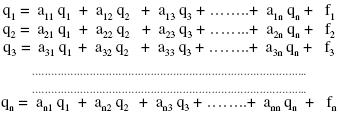
que, expresado en forma matricial, se reduce a:
q = Aq + f
donde la matriz A es la matriz de coeficientes cuyo elemento típico es aij.
Hasta ahora, el sistema no es más que una forma contable de representación de flujos en la matriz de Insumo–Producto y no se ha postulado ningún comportamiento económico. Sin embargo, si se piensa en este sistema como un sistema de ecuaciones que representa el funcionamiento de una economía y se hace el supuesto de que los sectores operan con funciones de producción que no permiten sustituibilidad entre insumos (coeficientes aijfijos), podemos entonces imaginar que el sistema describe la formación de la oferta y demandas. Se tiene entonces la representación de un modelo económico en el que los precios de los factores son fijos.
Este sistema tiene la siguiente solución:

donde la matriz B es conocida como la matriz inversa de Leontief o matriz de multiplicadores (análoga al multiplicador keynesiano).
La matriz B = (I –A)–1 es fundamental en el análisis insumo–producto, pues muestra los impactos totales de la demanda de producto de cada sector en el resto de los sectores. Es decir, esta matriz tiene características análogas a las del multiplicador keynesiano pues permite incorporar la interdependencia tecnológica del sistema productivo y rastrear la generación de la demanda final hacia atrás en el sistema. Entonces permite calcular cuánta producción se requiere para atender diversos niveles de demanda final y, en consecuencia, cómo deberían cambiar los niveles de producción para satisfacer esos cambios en la demanda final, los que pueden provenir de, por ejemplo, aumentos en los montos de inversión, pública y/o privada, además de otros componentes de la demanda final. Nótese que, en la medida en que se pueden estimar los niveles de producción requeridos en todos los sectores para satisfacer el cambio en la demanda final, se pueden también estimar los requerimientos de insumos, empleo e ingreso de todos los sectores.
4.3.4. Regla de Cromer.
Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede utilizar cuando la matriz A de coeficientes del sistema es cuadrada y de determinante no nulo. El que A sea cuadrada significa que el numero de incógnitas y el numero de ecuaciones coincide.
Cuando el sistema de ecuaciones:
satisface las condiciones arriba mencionadas, su solución viene dada por:
En general
donde A es la matriz que se obtiene sustituyendo la i-esima columna de A por la matriz de los terminos independientes, B
Ejemplo
Consideremos el sistema de ecuaciones:
En este sistema de ecuaciones lineales, la matriz A de los coeficientes es una matriz cuadrada y . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
https://www.youtube.com/watch?feature=player_embedded&v=gHpUcMr5rt8
4.3.3.Propiedades de las determinantes
4.3.3.Propiedades de las determinantes
Métodos de solución a sistemas de ecuaciones lineales
Sustitución
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente y a continuación sustituirla en otra ecuación por su valor.
En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita  por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
El siguiente paso será sustituir cada ocurrencia de la incógnita  en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.
Al resolver la ecuación obtenemos el resultado 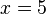 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 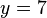 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.
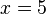 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos 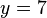 , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.Igualación
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita  en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:
Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Una vez obtenido el valor de la incógnita  , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
 , se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la
, se sustituye su valor en una de las ecuaciones originales, y se obtiene el valor de la  .
.
La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Reducción
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.
Por ejemplo, en el sistema:
No tenemos más que multiplicar la primera ecuación por 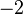 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
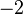 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así:
Si sumamos esta ecuación a la segunda del sistema original, obtenemos una nueva ecuación donde la incógnita  ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
 ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
:
El siguiente paso consiste únicamente en sustituir el valor de la incógnita  en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:
 en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  si sustituimos en la primera ecuación es igual a:
si sustituimos en la primera ecuación es igual a:4.3.2. Expanción por cofactores.
Se puede probar el siguiente:
Teorema
Todo determinante es igual a la suma de los productos de los elementos de un renglón (o columna) cualquiera por sus cofactores correspondientes.
Esto es
 (2) (2)
es el desarrollo del determinante D por el renglón i, y similarmente
es el desarrollo del determinante D por la columna k.
|
Las expresiones (2) y (3) son fórmulas completamente generales, cualquier determinante de cualquier dimensión se puede evaluar usando estas fórmulas.
Ejemplo 3.
Desarrollar por cofactores del segundo renglón y calcular el valor del determinante D.

Para expandir D, por cofactores del segundo renglón, calculamos primero los cofactores A21, A22 y A23 de los elementos del segundo renglón.
Entonces:
4.3.1. Definición de una determinante:
4.3.1. Definición de una determinante:
En Matemáticas se define el determinante como una forma multi-lineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos. Sin embargo, el concepto de determinante o de volumen orientado fue introducido para estudiar el número de soluciones de los sistemas de ecuaciones lineales.
4.3. Determinantes.
4.3. Determinantes.
https://www.youtube.com/watch?feature=player_embedded&v=sS-vy-es0j0
A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por |A| o por det (A).
|A| = 
A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A, denotado por |A| o por det (A).
|A| = 

Determinante de orden uno
|a11| = a11
Ejemplo
|5| = 5
|a11| = a11
Ejemplo
|5| = 5
Determinante de orden dos
 = a 11 a 22 − a 12 a 21
Ejemplo
= a 11 a 22 − a 12 a 21
Ejemplo

 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21
Ejemplo


Determinante de orden tres
Consideremos una matriz 3x3 arbitraria A = (aij). El determinante de A se define como sigue:
 =
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 −
− a13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 −
− a13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).
Ejemplo
 =
3 · 2 · 4 + 2 · (−5) · (−2) + 1 · 0 · 1 −
− 1 · 2 · (−2) − 2 · 0 · 4 − 3 · (−5) · 1 =
= 24 + 20 + 0 − (−4) − 0 − (−15) =
= 44 + 4 + 15 = 63
=
3 · 2 · 4 + 2 · (−5) · (−2) + 1 · 0 · 1 −
− 1 · 2 · (−2) − 2 · 0 · 4 − 3 · (−5) · 1 =
= 24 + 20 + 0 − (−4) − 0 − (−15) =
= 44 + 4 + 15 = 63
Consideremos una matriz 3x3 arbitraria A = (aij). El determinante de A se define como sigue:
 =
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 −
− a13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).
Ejemplo
 =
=
 =
=
3 · 2 · 4 + 2 · (−5) · (−2) + 1 · 0 · 1 −
− 1 · 2 · (−2) − 2 · 0 · 4 − 3 · (−5) · 1 =
= 24 + 20 + 0 − (−4) − 0 − (−15) =
= 44 + 4 + 15 = 63
4.2.4. Matriz inversa.
4.2.4. Matriz inversa.
Si premultiplicamos (multiplicamos por la izquierda) o posmultiplicamos (multiplicamos por la derecha) una matriz cuadrada por su inversa obtenemos la matriz identidad.
A · A−1 = A−1 · A = I
Propiedades
1 (A · B)−1 = B−1 · A−1
2 (A−1)−1 = A
3 (k · A)−1 = k−1 · A−1
4 (At)−1 = (A−1)t
Cálculo por el método de Gauss
Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A−1, seguiremos los siguientes pasos:
1 Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.
Consideremos una matriz 3x3 arbitraria:

Cálculo por el método de Gauss
Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A−1, seguiremos los siguientes pasos:
1 Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha.
Consideremos una matriz 3x3 arbitraria:

La ampliamos con la matriz identidad de orden 3.

2 Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A−1.
F2 = F2 − F1

F3 = F3 + F2

F2 = F2 − F3

F1 = F1 + F2

F2 = (−1) F2

La matriz inversa es:

https://www.youtube.com/watch?feature=player_embedded&v=TbIE7ncn8Ag
Suscribirse a:
Entradas (Atom)